探索科学的魅力高中物理必修二中的双星模型解析 想象一下，你手中转笔的两端，随着笔尖的灵动舞动，仿佛在演绎着双星的奇妙旅程双星模型，这个看似平凡的日常现象，实则是宇宙物理学中一个精妙的力学模型两颗恒星，如同笔的两端，围绕着共同的引力中心，以各自独特的轨道稳定旋转，这就是双星系统的核；要注意统一参考系，正确判断矢量的方向能量转化陷阱要注意非保守力如摩擦力做功时机械能不守恒，以及闭合回路中电能与热能的分配关系总结建议 结合典型题型如斜面问题含容电路双星模型等深化理解，注重公式的适用条件而非死记硬背通过多做题多总结，不断提高解题能力和物理素养。

高中物理双星模型(高中物理双星模型公式推导) 第1张

实际应用双星模型在天文学中有广泛的应用，例如可以用来解释双星系统的运动规律估算双星系统的质量等综上所述，双星模型是一个描述两个星体通过万有引力相互吸引并围绕共同圆心做匀速圆周运动的物理模型在这个模型中，万有引力提供向心力，且两个星体的运动特性与它们的质量密切相关；如线速度$v = omega r$，加速度$a = omega^2r$等，在双星系统中同样适用综上所述，双星模型是一个描述两颗恒星通过万有引力相互作用，在共同的质心周围稳定运动的物理模型它涉及质量运动半径引力角速度速度和加速度等多个物理量，并可以通过已知的物理量计算出其他未知的物理量。

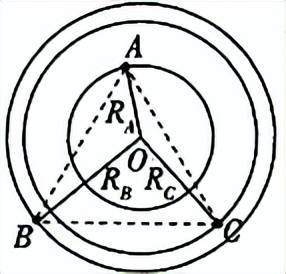
高中物理必修二中的双星模型是一个描述两颗恒星围绕共同引力中心旋转的力学模型以下是 双星模型的关键点解析核心概念两颗恒星围绕共同的引力中心旋转它们之间的万有引力相互作用，保持同步旋转，具有相同的周期T和角速度ω质量与轨道半径的关系恒星间的引力与它们的质量和轨道半径的平方成反比；所需向心力同样由万有引力提供在处理多星模型时，需注意几个易错点在万有引力公式中，公式 和 公式 分别代表两个星体间的距离向心加速度公式中的公式 和 公式 则指星体做匀速圆周运动的轨道半径在双星模型与多星模型中，星体间的距离与轨道半径应正确区分，避免混淆。

双星三星模型，宇宙中奇妙景象，探讨其周期线速度，理解模型特点，突破重难点双星系统，围绕公共圆心旋转的两个星体组成，特性独特，需掌握求解周期线速度方法三星模型分为两种情况，三颗星连在同一直线，两颗星围绕中央星在同一半径圆轨道运行知识点与技巧，分享学习方法，助力高效备考，提升物理；高中物理剖析宇宙中的双星三星模型，考点突破，分数稳拿一双星模型 双星模型是指绕公共圆心转动的两个星体组成的系统这种系统有以下特点稳定性双星系统通常处于动态平衡状态，即两个星体以相同的角速度绕公共圆心旋转万有引力提供向心力两个星体之间的万有引力是它们做圆周运动所需的向心力由于它们之间的距离保持不变，因。

高中物理双星模型公式总结

1、物理模型不少的啊，有些模型一个知识点有好一个对应的模型，有些模型要用到好多知识点的只能想起来啥说啥了力学中小船过河模型，人船模型，竖直内圆模型，子弹木块模型，碰撞模型完全弹性碰撞完全非弹性碰撞双星模型高低轨模型电学电场中的类平抛洛伦兹力作用下的圆周运动。

2、高中物理解题技巧知识点总结天体运动 一处理天体问题的基本思路与规律 建立模型天体运动问题通常首先需要建立模型，如假设天体做匀速圆周运动，此时万有引力提供向心力利用公式在建立模型后，利用天体表面和空间轨道上的代换关系等公式进行求解常见的公式包括万有引力定律向心力公式等二人造。

高中物理双星模型(高中物理双星模型公式推导) 第2张

3、一般双星系的两星的角速度相同，而万有引力大小相同，所以旋转半径之比是两星球质量的反比即R1R2=m2m1万有引力是两个星体之间的要代L ，若A星体距离该点距离为r，设两星体的质量都为m，则对A有GmmL^2=mv^2r 注意向心力的半径为r， 对B星体有GmmL^2=mv^2Lr是GMmL^2。

4、高中物理必修二·双星模型详解当笔两端转笔时，这个现象实际上展示了双星模型的基本原理，即两颗恒星通过万有引力相互作用在共同的质心周围稳定运动让我们深入理解这个模型双星系统由两颗恒星组成，它们的质量分别用公式和公式表示，各自围绕共同中心做周期相同的匀速圆周运动每个恒星的运动半径与其。

高中物理双星模型公式推导

1、模型则在于应用，它填补理论的空白，让你的方程完整比如在万有引力章节，学习各种模型如变轨问题和双星模型，单纯记忆公式和做题并不能真正理解其内涵，模型的意义在于实际解决问题的能力学姐特别为高中生精心整理了100张 高中物理三年所有定义公式和模型的全面知识点总结，电子版可供打印由于篇幅。

2、两个长度分别是两个粒子做圆周运动的半径但是需要提及一点，也是双星模型中唯一重点，他们的引力在这里是库仑力，在其他题目可能就是万有引力，中的距离是L，而不是那两个半径高中物理学习很多题目是一样的，特别是力学与电学是最贴近的不是电学与磁学，很多初学者会弄混淆，电学与力学是最。

3、有两种情况一种是两个星球的引力提供向心力并且绕着其中的某一个星球旋转半径就是两个星球的距离然后用公式就行了一种是绕着两个星球的连线上的某一点旋转半径比其间的距离小，有关系R1+R2=L用公式 就。