1、你好是否必须保持立体图形三视图边的长度与原直观图一致,并非绝对以一个正三棱锥为例,其主视图中的边长应当与直观图中的边长相等,但侧视图则应反映直观图的高度三视图包括主视图俯视图和侧视图,分别从物体的前后上下左右三个方向进行投影主视图是从前向后看,侧视图是从左向右看,俯;柱体上下底面平行且全等,侧面为矩形直柱体或平行四边形斜柱体锥体底面为多边形,侧面为三角形,顶点在底面的投影为垂足直锥体或非垂足斜锥体台体用平行于底面的平面截锥体,截面与底面间的部分称为台体球体空间中到定点的距离等于定长的点的集合三视图与直观图 三;这个有几个办法其一,凭借三维想象空间能力其二,用临场的书,纸动手操作一下其三,用手指和一支笔来模拟其四,排除法,先排除肯定不可能出现的视图的选项后面的都是一些为追求分数而设的答题技巧了 画。

2、高中数学三视图可以这样看正面看想象一下你正对着物体站着,眼睛直视前方,这时你看到的物体的形状就是正视图啦比如圆锥的正视图就是一个三角形侧面看接着,你转到物体的侧面,像是一个旁观者一样,这时你看到的形状就是侧视图还是拿圆锥来说,它的侧视图也是一个三角形哦上面看最后;高中数学中的三视图,主要是从正面侧面和上面三个方向来观察并描绘一个立体图形的投影图形从正面看正视图是从物体的正面投射而来的视图在这个视角下,我们需要想象自己站在物体的正前方,垂直看向物体例如,一个圆锥的正视图会呈现为一个三角形,因为从正面看,圆锥的侧面展开后就是一个三角形;一核心原理利用长方体正方体作为空间坐标系框架选择 根据三视图中最大轮廓尺寸,确定一个 所有几何元素的长方体或正方体作为“容器”例如若三视图显示长宽高分别为321,则选择3×2×1的长方体为框架坐标定位法 将长方体的8个顶点视为三维坐标系的原点0,0,0及延伸点;左边是半圆锥,右边也是半圆锥,左右对称左边;高中数学中的三视图,主要是从正面侧面和上面三个不同方向观察一个立体图形所得到的平面图形正视图定义从物体的正面投影所得到的视图观察角度正面垂直看向物体示例如圆锥的正视图通常是一个三角形,显示其底面或顶面的投影形状侧视图定义从物体的侧面投影所得到的视图观察角度;高中数学公式大全5立体几何空间向量一直观图三视图正视图侧视图俯视图长对正,高平齐,宽相等直观图通过斜二测画法得到,直观图与原图形面积之间存在一定的比例关系二表面积体积圆柱侧面展开图矩形侧面积公式$S_侧 = 2pi rh$$r$为底面半径,$h$为高表。
3、从简单的体,比如三棱柱,三棱锥,去尝试画它的三视图,画多了就熟练了需要一定的空间想象能力以下再从百度摘一下三视图的定义三视图是观测者从三个不同位置观察同一个空间几何体而画出的图形将人的视线规定为平行投影线,然后正对着物体看过去,将所见物体的轮廓用正投影法绘制出来该图形称为;高中数学中的三视图需要从正面侧面和上面三个方向进行观察和理解正视图正视图是从物体的正面所看到的图形在观察时,想象光线从正面垂直照射到物体上,并投影到一个与物体正面平行的平面上例如,圆锥的正视图通常是一个三角形侧视图侧视图是从物体的侧面所看到的图形同样地,想象光线从侧;比如圆锥的正视图是三角形,侧面也是三角形,俯视图是圆,那就想像出一个无限长的三棱柱,用一个与之垂直的三棱柱去截它,然后再用一个圆柱去截,这样就得到一个立体的圆锥了我们必须得要有丰富的想象力,然后分别从正面侧面上面来想象他们的图形,这样就完成一个图形的三视;高中数学中的三视图主要通过从正面侧面和上面三个不同方向观察物体,并想象或绘制出相应的平面图形来理解一正面视图正视图正视图是从物体的正面通常指观察者面对的方向投射所得的视图它展示了物体在该方向上的形状和尺寸例如,一个圆锥的正视图通常是一个三角形,因为它在正面方向上看起来就像一个三角形二侧面视图侧视图侧视图。
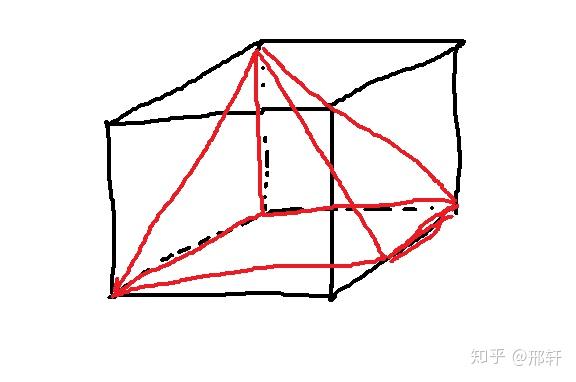
4、在处理这样的几何问题时,首先需要明确被切割的几何体的原始形状这里提到的是一个正方体,它被切割成了一个三棱柱半个正方体,并在三棱柱的基础上进一步切去了一个三棱锥ABCD为了准确地还原切割后的三视图,我们首先需要理解切割过程三棱柱是正方体的一半,因此它的底面和顶面都是正方形的一半,侧面是矩形接下来,三棱锥ABC;高中数学中的三视图,需要从正面侧面和上面三个方向来观察和想象图形的形状正视图定义从物体的正面投影得到的视图观察方法想象自己站在物体的正前方,垂直看向物体,此时看到的形状即为正视图侧视图定义从物体的侧面投影得到的视图观察方法想象自己站在物体的侧面,垂直看向物体。


发表评论